읽는데 약 3분
[백준 21234] Just Green Enough
문제
https://www.acmicpc.net/problem/21234
알고리즘
스위핑
풀이
N * N 사각형안에 값들이 주어집니다. 부분 직사각형안에 최솟값이 100이 될 수 있는 직사각형의 갯수를 구하는 문제입니다.
사각형을 결정하기 위해선 상하좌우의 변이 필요합니다. 다르게 말하자면 브루트포스로 해결하기 위해선 $O(N^4)$의 시간복잡도가 필요하므로 시간초과입니다. 한 직사각형의 위와 왼쪽변을 결정했다고 가정하겠습니다. 이 변들을 포함하며 최솟값이 100이 되는 직사각형들을 찾기 위해서는 왼쪽변보다 오른쪽에 위치한 변들을 살피며 그때 아래변들을 살펴보면 됩니다. 이 과정은 위에서 언급한대로 $O(N^4)$의 시간복잡도를 필요하지만 아래변들을 살필 때 우리가 찾는 것은 가장 높은 100의 위치(A)와 포함해서는 안되는 위치(B)입니다. 이를 계산할 수 있다면 위, 왼쪽, 오른쪽 변에 해당하는 i, j, k를 포함하며 최솟값이 100인 직사각형을 B-A를 통해 구할 수 있습니다.
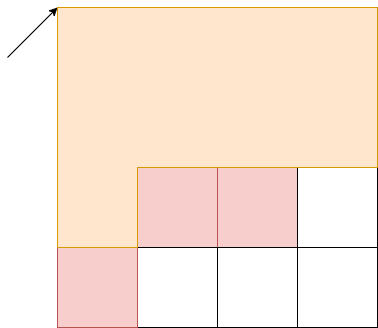
그림을 통해 다시 보겠습니다. 빨간색 부분은 포함해서는 안되는 부분입니다. 예를 들어 화살표가 가리키는 부분이 맨 위의 변과 왼쪽변을 가리키는 i, j라고 하면 우측변 k마다 top100[i][k]값을 알고 있다면 topdark[i][k]와 top100[i][k]의 값을 빼면 i,j,k 변에서 만들 수 있는 직사각형의 갯수를 바로 구할 수 있습니다. 이 행동을 k가 맨 오른쪽에 도달할때까지 한다면 $O(N^3)$에 원하는 값을 구할 수 있습니다. 유의할점은 다음과 같은 상황입니다.
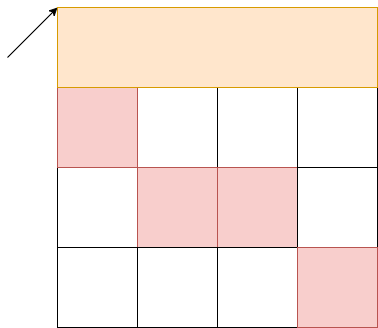
k의 초반에 포함해서는 안되는 사각형의 위치를 topdark[i][k]로 구하고 계산한 다음, k+1단계에서 topdark를 구할때는 이전에 topdark[i][k]값을 고려해야한다는 것입니다.
코드1
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < n; ++i)
#define REP(i, n) for (int i = 1; i <= n; ++i)
using namespace std;
int N;
int board[500][500];
int top100[500][500];
int topdark[500][500];
int main() {
#ifndef ONLINE_JUDGE
freopen("in", "r", stdin);
freopen("out", "w", stdout);
#endif
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
cin >> N;
rep(i, N) rep(j, N) {
top100[i][j] = N;
topdark[i][j] = N;
}
rep(i, N) rep(j, N) {
cin >> board[i][j];
}
rep(i, N) rep(j, N) {
for (int k = 0; k <= i; ++k) {
if (board[i][j] == 100) {
top100[k][j] = min(top100[k][j], i);
} else if (board[i][j] < 100) {
topdark[k][j] = min(topdark[k][j], i);
}
}
}
long long ans = 0;
rep(i, N) rep(j, N) {
int a = N;
int b = N;
for (int k = j; k < N; ++k) {
a = min(top100[i][k], a);
b = min(topdark[i][k], b);
if (b - a > 0) {
ans += b - a;
}
}
}
cout << ans;
return 0;
}
코드2(USACO)
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < n; ++i)
#define REP(i, n) for (int i = 1; i <= n; ++i)
using namespace std;
bool ok[500][500];
int N;
int board[500][500];
long long ans = 0;
long long solve() {
long long ret = 0;
rep(i, N) {
vector<bool> jup(N, 1);
for (int j = i; j < N; ++j) {
int cnt = 0;
for (int k = 0; k < N; ++k) {
jup[k] = jup[k] & ok[j][k];
if (jup[k])
ret += ++cnt;
else
cnt = 0;
}
}
}
return ret;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("2.in", "r", stdin);
freopen("out", "w", stdout);
#endif
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
cin >> N;
rep(i, N) rep(j, N) cin >> board[i][j];
rep(i, N) rep(j, N) ok[i][j] = (board[i][j] >= 100);
ans += solve();
rep(i, N) rep(j, N) ok[i][j] = (board[i][j] > 100);
ans -= solve();
cout << ans;
return 0;
}